CPM geometry answers are key to unlocking complex geometric concepts. This guide delves into the fundamentals of CPM geometry, exploring problem-solving techniques, theorems, postulates, and real-world applications. From understanding basic shapes to tackling advanced problems, we provide a comprehensive resource for students navigating the challenges of CPM geometry.
We’ll examine various problem types, including those involving angles, triangles, circles, and more. The guide features detailed explanations, illustrative examples, and step-by-step solutions to help readers master the core concepts. We’ll also discuss the importance of accurate diagrams and the use of tools like compasses and straightedges for geometric constructions. Finally, we’ll explore how these concepts apply to fields like architecture and engineering.
Understanding CPM Geometry
CPM geometry, often encountered in high school mathematics, builds upon foundational geometric concepts to solve complex problems. It emphasizes a problem-solving approach, encouraging students to analyze, reason, and visualize geometric relationships. This section will delve into the core principles of CPM geometry, illustrating various problem types and effective solution strategies.
Fundamental Concepts of CPM Geometry
CPM geometry rests on the pillars of Euclidean geometry, incorporating concepts like points, lines, planes, angles, triangles, quadrilaterals, circles, and three-dimensional shapes. Understanding congruence, similarity, and transformations is crucial. The ability to identify and apply geometric properties, such as parallel lines, perpendicular lines, and angle relationships, is fundamental to problem-solving.
Examples of CPM Geometry Problems
CPM geometry problems range from simple angle calculations to complex proofs involving multiple geometric figures and theorems. Examples include finding the area of irregular shapes, determining the lengths of sides in similar triangles, proving the congruence of triangles, and calculating volumes of three-dimensional objects. Problems often involve a combination of algebraic and geometric reasoning.
Steps Involved in Solving CPM Geometry Problems
A systematic approach is key to solving CPM geometry problems. This typically involves: 1) Carefully reading and understanding the problem statement; 2) Drawing an accurate diagram; 3) Identifying relevant geometric properties and theorems; 4) Developing a plan to solve the problem; 5) Executing the plan, showing all steps; and 6) Checking the solution for reasonableness.
Students struggling with CPM geometry answers might find supplemental resources online, but be wary of unreliable sources. For a different kind of resource check out fortwayne craigslist for used textbooks or tutoring services; you might find a local tutor offering help with CPM geometry answers. Remember to always verify the credibility of any assistance you find, whether online or offline, to ensure academic integrity.
Strategies for Identifying Relevant Geometric Properties
Effective problem-solving relies on recognizing relevant geometric properties. This involves careful observation of the diagram, noting parallel lines, perpendicular lines, congruent angles or segments, similar triangles, and other key relationships. Familiarity with geometric theorems and postulates is crucial in making these identifications.
Comparison of CPM Geometry Problem Types
| Problem Type | Key Concepts | Solution Steps | Example Problem |
|---|---|---|---|
| Triangle Congruence | SSS, SAS, ASA, AAS postulates | Identify corresponding parts, apply appropriate postulate | Prove that two triangles with two sides and the included angle equal are congruent. |
| Similar Triangles | AA, SSS, SAS similarity theorems | Establish similarity, use ratios of corresponding sides | Find the height of a tree using similar triangles and shadow lengths. |
| Area Calculations | Formulas for area of various shapes | Identify shape, apply appropriate formula | Calculate the area of a trapezoid given its bases and height. |
| Volume Calculations | Formulas for volume of various 3D shapes | Identify shape, apply appropriate formula | Find the volume of a cone given its radius and height. |
Analyzing CPM Geometry Theorems and Postulates
Theorems and postulates form the bedrock of geometric reasoning. Understanding their applications is essential for solving complex problems. This section will explore key theorems and postulates, illustrating their use in various problem-solving contexts.
Key Theorems and Postulates in CPM Geometry
Fundamental theorems and postulates include the Pythagorean Theorem (relating the sides of a right-angled triangle), the Triangle Angle Sum Theorem (stating the sum of angles in a triangle is 180 degrees), parallel postulate (through a point not on a line, there is exactly one parallel line), and various congruence postulates (SSS, SAS, ASA, AAS).
Application of Theorems and Postulates to Problem-Solving
Theorems and postulates provide the logical framework for solving geometric problems. For example, the Pythagorean Theorem allows us to calculate the length of an unknown side in a right-angled triangle, while the Triangle Angle Sum Theorem helps determine unknown angles. Congruence postulates are used to prove the congruence of triangles, which can then be used to establish other relationships within a figure.
Examples of Theorem and Postulate Application
Consider a problem involving a right-angled triangle where two sides are known. The Pythagorean Theorem can be applied to find the length of the third side. In a problem involving parallel lines intersected by a transversal, corresponding angles are shown to be congruent using the parallel postulate.
Flowchart for Applying Theorems and Postulates
A flowchart could illustrate the logical steps: 1) Identify the given information; 2) Identify the desired outcome; 3) Determine relevant theorems/postulates; 4) Apply theorems/postulates; 5) Draw conclusions; 6) Verify the solution.
Categorization of Theorems and Postulates
- Triangle Properties: Triangle Angle Sum Theorem, Pythagorean Theorem, Triangle Inequality Theorem
- Parallel Lines: Corresponding Angles Theorem, Alternate Interior Angles Theorem, Consecutive Interior Angles Theorem
- Congruence: SSS, SAS, ASA, AAS postulates
- Similarity: AA, SSS, SAS similarity theorems
Solving Different Types of CPM Geometry Problems
This section will detail common problem types, comparing solution methods and providing step-by-step solutions for progressively challenging problems. Tips and tricks for efficient problem-solving will also be shared.
Common Problem Types in CPM Geometry
Common problem types include those involving triangles (congruence, similarity, area, angles), quadrilaterals (properties, area), circles (circumference, area, arc length), and three-dimensional shapes (volume, surface area). Problems often involve combining multiple concepts.
Comparison of Solution Methods
Different problem types may require different solution methods. For instance, finding the area of a triangle might involve using the formula 1/2
– base
– height, while finding the area of a circle requires the formula πr². Solving for unknown angles in a triangle might involve using the Triangle Angle Sum Theorem.
Step-by-Step Solution of a Complex Problem
Let’s consider a problem involving a complex shape formed by combining a rectangle and a triangle. The solution would involve breaking down the shape into simpler components, calculating the area of each component using appropriate formulas, and then adding the areas to find the total area.
Series of Progressively Challenging Problems
- Find the area of a triangle with base 6 cm and height 4 cm.
- Find the length of the hypotenuse of a right-angled triangle with legs of length 3 cm and 4 cm.
- Find the area of a trapezoid with bases of length 5 cm and 7 cm and height 3 cm.
- Find the volume of a rectangular prism with length 5 cm, width 4 cm, and height 3 cm.
Tips and Tricks for Efficient Problem-Solving
- Draw accurate diagrams.
- Label all known quantities.
- Identify relevant theorems and postulates.
- Work systematically, showing all steps.
- Check your solution for reasonableness.
Visualizing and Representing CPM Geometry Solutions
Accurate geometric diagrams are crucial for visualizing problems and solutions. This section will emphasize the importance of diagrams, exploring tools and techniques for creating clear and concise representations of geometric concepts.
Importance of Accurate Geometric Diagrams
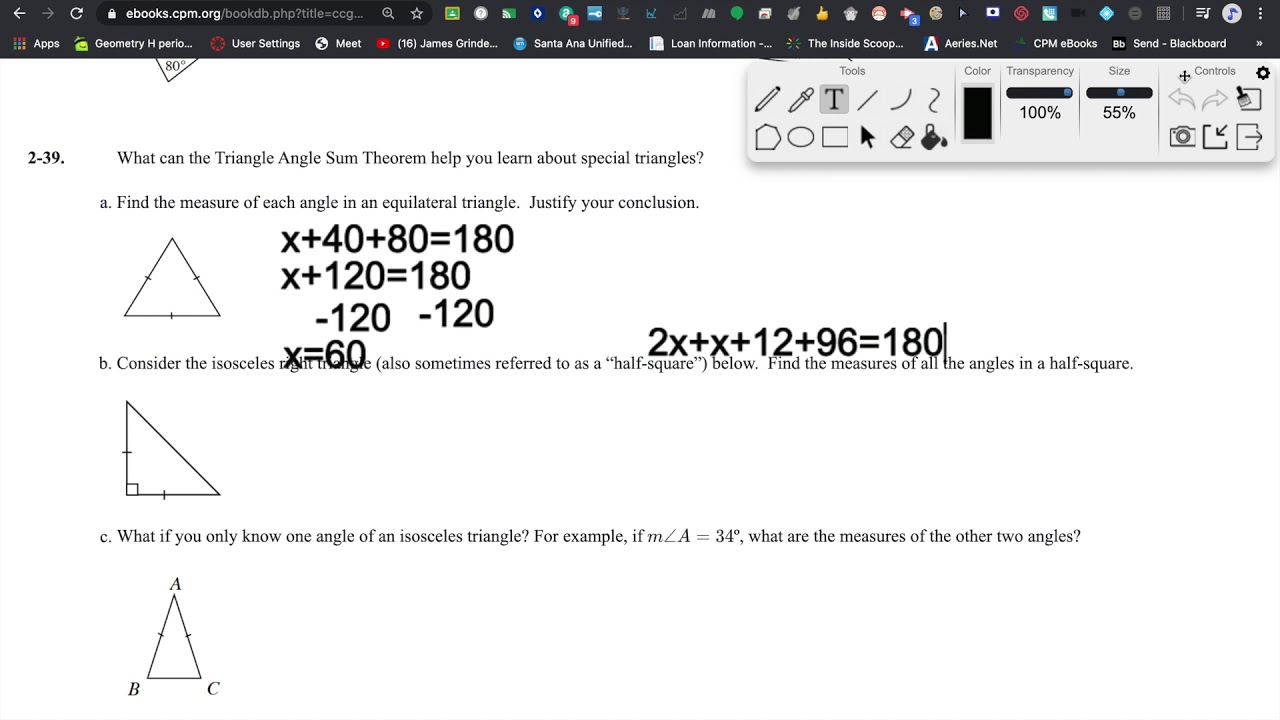
Source: ytimg.com
Accurate diagrams help visualize geometric relationships, making it easier to identify relevant properties and theorems. A well-drawn diagram serves as a roadmap for solving the problem, guiding the logical steps involved.
Tools and Techniques for Creating Geometric Diagrams
Tools such as rulers, compasses, protractors, and geometry software can be used to create accurate diagrams. Hand-drawn diagrams should be neat and clearly labeled, while software allows for precise construction and manipulation of geometric figures.
Detailed Diagram Illustrating a Problem and Solution
Imagine a problem involving two similar triangles. A diagram would show the two triangles, clearly labeling corresponding angles and sides. The solution would involve setting up ratios of corresponding sides to find unknown lengths. The diagram would visually demonstrate the similarity and the calculations performed.
Tips for Creating Clear and Concise Diagrams
- Use a ruler and compass for precise constructions.
- Label all points, lines, angles, and segments clearly.
- Use different colors or line styles to distinguish different parts of the diagram.
- Keep the diagram neat and uncluttered.
Step-by-Step Guide for Geometric Constructions
Constructing a perpendicular bisector involves drawing a circle with a compass centered at each endpoint of a line segment, with the radius greater than half the segment length. The intersection points of the circles determine the perpendicular bisector.
Applying CPM Geometry Concepts to Real-World Scenarios: Cpm Geometry Answers

Source: ytimg.com
CPM geometry finds widespread application in various fields. This section will explore real-world applications, demonstrating how geometric principles are used to solve practical problems.
Real-World Applications of CPM Geometry
CPM geometry is essential in architecture (designing buildings, calculating structural stability), engineering (designing bridges, roads, and other structures), and design (creating aesthetically pleasing and functional objects). It is also used in surveying, cartography, and computer graphics.
CPM Geometry in Different Fields
Architects use geometry to ensure buildings are structurally sound and aesthetically pleasing. Engineers use geometry to design and analyze structures, ensuring stability and safety. Designers use geometry to create visually appealing and functional products.
Examples of Real-World Problems Solved Using CPM Geometry
Calculating the height of a building using similar triangles and shadow lengths, determining the area of a plot of land for construction, or designing a support structure for a bridge using geometric principles are all examples of real-world applications.
Translating Real-World Problems into CPM Geometry Problems, Cpm geometry answers
This involves identifying the relevant geometric shapes and relationships within the real-world problem, representing these relationships using a diagram, and then applying appropriate geometric principles to solve for the unknown quantities.
Case Study: Applying CPM Geometry to Architecture
Consider designing a roof for a building. The architect would use geometry to determine the angles of the roof slopes, the lengths of the rafters, and the overall dimensions to ensure stability and water runoff. The design would incorporate geometric principles to create a functional and aesthetically pleasing structure.
Final Wrap-Up
Mastering CPM geometry requires a solid understanding of fundamental concepts, a systematic approach to problem-solving, and the ability to visualize geometric relationships. This guide has provided a roadmap to navigate the intricacies of CPM geometry, equipping readers with the tools and strategies needed to tackle even the most challenging problems. By applying the techniques and insights presented here, students can confidently approach geometry problems with increased understanding and efficiency, ultimately achieving a deeper appreciation for the elegance and power of geometric principles.
